Sorting Algorithms
This is the last blog post that I will be writing for CSC148H1F. I want to take this opportunity to say that I really enjoyed Danny's pedagogical methods in this course.
In this post, I'll be talking about a few sorting algorithms and talk about their efficiency and how they can be improved.
Selection Sort:
Lets say we want to sort a list of n elements. At each step we assume the first 'k' elements are already sorted. Then we look at the rest 'n-k' elements, find the smallest element, and put it at the 'k+1'st position.
Efficiency:
So we first go through n-1 elements, then n-2 elements, then n-3 elements, ..., 2 elements, and 1 element. Hence, the runtime of this algorithm is O(n^2). But this is very inefficient since we make many unnecessary comparisons.
Implementation:
The following is the code that was provided in lab #9 for selection sort:
def find_min(L, i):
"""Return the index of the smallest item in L[i:]."""
smallest = i
for j in range(i + 1, len(L)):
if L[j] < L[smallest]:
smallest = j
return smallest
# find_min using built-in min, tuple comparisons, and enumerate
# should be faster...
#def find_min(L, i):
#"""Return index of smallest item in L[i:]."""
#return min([(k, j) for j, k in enumerate(L[i:])])[1] + i
def selection_sort(L):
"""Sort the items in L in non-decreasing order."""
i = 0
while i != len(L) - 1:
# Find the smallest remaining item and move it to index i.
smallest = find_min(L, i)
L[smallest], L[i] = L[i], L[smallest]
i += 1
Merge Sort:
We all learned about merge sort algorithm in class as one of our main examples for a divide and conquer algorithm. As we can see in lab 9, it can be implemented in two ways.
1) You can divide the list into two parts, call merge sort on both of them, and then merge the two sorted lists.
2) The second method is what you would call an in place sort. In this method, instead of making copies of each part of the list and sorting them, you do the sort process on the initial list, hence the name. This method significantly reduces the amount of memory that is used by the program.
Efficiency:
The runtime of merge sort is of order O(n lg n). Because we divide the problem lg n times and in each step of merging, we make at most n comparisons.
There is no significant difference between the runtime of the first and second methods. It is mainly the memory usage that differs.
Implementation:
The following is the implementation for both methods. The code if from lab 9:
############ Mergesort 1 ############
def _merge_1(left, right):
"""Merge sorted lists left and right into a new list and return that new
list."""
result = []
i ,j = 0, 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result
def _mergesort_1(L):
"""Return a new list that is a sorted version of list L."""
if len(L) < 2:
return L
else:
middle = len(L) // 2
left = _mergesort_1(L[:middle])
right = _mergesort_1(L[middle:])
return _merge_1(left, right)
def mergesort_1(L):
"""Sort list L."""
L[:] = _mergesort_1(L)
############ Mergesort 2 ############
def _merge_2(L, i, mid, j):
"""Merge the two sorted halves L[i:mid + 1] and L[mid + 1:j + 1] and return
them in a new list. Notice that L[mid] belongs in the left half and L[j]
belongs in the right half -- the indices are inclusive."""
result = []
left = i
right = mid + 1
# Done when left > mid or when right > j -- we've finished one of the
# halves.
while left <= mid and right <= j:
if L[left] < L[right]:
result.append(L[left])
left += 1
else:
result.append(L[right])
right += 1
# Items left: L[left:mid + 1]
# L[right:j + 1]
return result + L[left:mid + 1] + L[right:j + 1]
def _mergesort_2(L, i, j):
"""Sort the items in L[i] through L[j] in non-decreasing order."""
if i < j:
mid = (i + j) // 2
_mergesort_2(L, i, mid)
_mergesort_2(L, mid + 1, j)
L[i:j + 1] = _merge_2(L, i, mid, j)
def mergesort_2(L):
"""Sort list L."""
_mergesort_2(L, 0, len(L) - 1)
Quick Sort:
Quick Sort was covered in class with a pretty lazy/elegant one-line implementation ("Python one-liners" <3). We were presented with 2 other implementations of quick sort in lab 9.
1) This one tries to do an in place quick sort, but it doesn't. The way the partitioning is done is cohesive with an in place quick sort algorithm. However, after the partitioning, we make a copy of the left side, and a copy of the right side and call quick sort on those two. (Ugh, so close to being an in place sort!)
2)This one though is very nice. It follows a similar pattern for partitioning, and does not make any additional copies of any part of the initial list. (Beautiful :') )
Efficiency:
Both of these alogrithms have a average case runtime of order O(n lg n). However, the second one, being an in place sort, save a whole lot on memory usage.
Implementation:
Here are the implementations from lab 9:
############ Quicksort 1 ############
def _partition_1(L):
"""Rearrange L so that items < L[0] are at the beginning and items >= L[0]
are at the end, and return the new index for L[0]."""
v = L[0]
i = 1
j = len(L) - 1
while i <= j:
if L[i] < v:
i += 1
else:
L[i], L[j] = L[j], L[i]
j -= 1
L[0], L[j] = L[j], L[0]
return j
def _quicksort_1(L):
"""Sort L by partitioning it around the first item, then recursing."""
if len(L) <= 1:
return L
else:
pivot = _partition_1(L)
left = L[:pivot]
right = L[pivot + 1:]
return _quicksort_1(left) + [L[pivot]] + _quicksort_1(right)
def quicksort_1(L):
"""Sort list L."""
L[:] = _quicksort_1(L)
# functional version
#def quicksort(L):
# if len(L) > 1 :
# return (quicksort([x for x in L[1:] if x < L[0]])
# + [L[0]] + quicksort([x for x in L[1:] if x >= L[0]]))
# else :
# return L
#
#def quicksort_1(L):
# L[:] = quicksort(L) # to sort original list
############ Quicksort 2 ############
def _partition_2(L, i, j):
"""Rearrange L[i:j] so that items < L[i] are at the beginning and items
>= L[i] are at the end, and return the new index for L[i]."""
v = L[i]
k = i + 1
j -= 1
while k <= j:
if L[k] < v:
k += 1
else:
L[k], L[j] = L[j], L[k]
j -= 1
L[i], L[j] = L[j], L[i]
return j
def _quicksort_2(L, i, j):
"""Sort L[i:j] by partitioning it around the first item, then recursing."""
if i < j:
pivot = _partition_2(L, i, j)
_quicksort_2(L, i, pivot)
_quicksort_2(L, pivot + 1, j)
def quicksort_2(L):
"""Sort list L."""
_quicksort_2(L, 0, len(L))
In this post, I'll be talking about a few sorting algorithms and talk about their efficiency and how they can be improved.
Selection Sort:
Lets say we want to sort a list of n elements. At each step we assume the first 'k' elements are already sorted. Then we look at the rest 'n-k' elements, find the smallest element, and put it at the 'k+1'st position.
Efficiency:
So we first go through n-1 elements, then n-2 elements, then n-3 elements, ..., 2 elements, and 1 element. Hence, the runtime of this algorithm is O(n^2). But this is very inefficient since we make many unnecessary comparisons.
Implementation:
The following is the code that was provided in lab #9 for selection sort:
def find_min(L, i):
"""Return the index of the smallest item in L[i:]."""
smallest = i
for j in range(i + 1, len(L)):
if L[j] < L[smallest]:
smallest = j
return smallest
# find_min using built-in min, tuple comparisons, and enumerate
# should be faster...
#def find_min(L, i):
#"""Return index of smallest item in L[i:]."""
#return min([(k, j) for j, k in enumerate(L[i:])])[1] + i
def selection_sort(L):
"""Sort the items in L in non-decreasing order."""
i = 0
while i != len(L) - 1:
# Find the smallest remaining item and move it to index i.
smallest = find_min(L, i)
L[smallest], L[i] = L[i], L[smallest]
i += 1
Merge Sort:
We all learned about merge sort algorithm in class as one of our main examples for a divide and conquer algorithm. As we can see in lab 9, it can be implemented in two ways.
1) You can divide the list into two parts, call merge sort on both of them, and then merge the two sorted lists.
2) The second method is what you would call an in place sort. In this method, instead of making copies of each part of the list and sorting them, you do the sort process on the initial list, hence the name. This method significantly reduces the amount of memory that is used by the program.
Efficiency:
The runtime of merge sort is of order O(n lg n). Because we divide the problem lg n times and in each step of merging, we make at most n comparisons.
There is no significant difference between the runtime of the first and second methods. It is mainly the memory usage that differs.
Implementation:
The following is the implementation for both methods. The code if from lab 9:
############ Mergesort 1 ############
def _merge_1(left, right):
"""Merge sorted lists left and right into a new list and return that new
list."""
result = []
i ,j = 0, 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result
def _mergesort_1(L):
"""Return a new list that is a sorted version of list L."""
if len(L) < 2:
return L
else:
middle = len(L) // 2
left = _mergesort_1(L[:middle])
right = _mergesort_1(L[middle:])
return _merge_1(left, right)
def mergesort_1(L):
"""Sort list L."""
L[:] = _mergesort_1(L)
############ Mergesort 2 ############
def _merge_2(L, i, mid, j):
"""Merge the two sorted halves L[i:mid + 1] and L[mid + 1:j + 1] and return
them in a new list. Notice that L[mid] belongs in the left half and L[j]
belongs in the right half -- the indices are inclusive."""
result = []
left = i
right = mid + 1
# Done when left > mid or when right > j -- we've finished one of the
# halves.
while left <= mid and right <= j:
if L[left] < L[right]:
result.append(L[left])
left += 1
else:
result.append(L[right])
right += 1
# Items left: L[left:mid + 1]
# L[right:j + 1]
return result + L[left:mid + 1] + L[right:j + 1]
def _mergesort_2(L, i, j):
"""Sort the items in L[i] through L[j] in non-decreasing order."""
if i < j:
mid = (i + j) // 2
_mergesort_2(L, i, mid)
_mergesort_2(L, mid + 1, j)
L[i:j + 1] = _merge_2(L, i, mid, j)
def mergesort_2(L):
"""Sort list L."""
_mergesort_2(L, 0, len(L) - 1)
Quick Sort:
Quick Sort was covered in class with a pretty lazy/elegant one-line implementation ("Python one-liners" <3). We were presented with 2 other implementations of quick sort in lab 9.
1) This one tries to do an in place quick sort, but it doesn't. The way the partitioning is done is cohesive with an in place quick sort algorithm. However, after the partitioning, we make a copy of the left side, and a copy of the right side and call quick sort on those two. (Ugh, so close to being an in place sort!)
2)This one though is very nice. It follows a similar pattern for partitioning, and does not make any additional copies of any part of the initial list. (Beautiful :') )
Efficiency:
Both of these alogrithms have a average case runtime of order O(n lg n). However, the second one, being an in place sort, save a whole lot on memory usage.
Implementation:
Here are the implementations from lab 9:
############ Quicksort 1 ############
def _partition_1(L):
"""Rearrange L so that items < L[0] are at the beginning and items >= L[0]
are at the end, and return the new index for L[0]."""
v = L[0]
i = 1
j = len(L) - 1
while i <= j:
if L[i] < v:
i += 1
else:
L[i], L[j] = L[j], L[i]
j -= 1
L[0], L[j] = L[j], L[0]
return j
def _quicksort_1(L):
"""Sort L by partitioning it around the first item, then recursing."""
if len(L) <= 1:
return L
else:
pivot = _partition_1(L)
left = L[:pivot]
right = L[pivot + 1:]
return _quicksort_1(left) + [L[pivot]] + _quicksort_1(right)
def quicksort_1(L):
"""Sort list L."""
L[:] = _quicksort_1(L)
# functional version
#def quicksort(L):
# if len(L) > 1 :
# return (quicksort([x for x in L[1:] if x < L[0]])
# + [L[0]] + quicksort([x for x in L[1:] if x >= L[0]]))
# else :
# return L
#
#def quicksort_1(L):
# L[:] = quicksort(L) # to sort original list
############ Quicksort 2 ############
def _partition_2(L, i, j):
"""Rearrange L[i:j] so that items < L[i] are at the beginning and items
>= L[i] are at the end, and return the new index for L[i]."""
v = L[i]
k = i + 1
j -= 1
while k <= j:
if L[k] < v:
k += 1
else:
L[k], L[j] = L[j], L[k]
j -= 1
L[i], L[j] = L[j], L[i]
return j
def _quicksort_2(L, i, j):
"""Sort L[i:j] by partitioning it around the first item, then recursing."""
if i < j:
pivot = _partition_2(L, i, j)
_quicksort_2(L, i, pivot)
_quicksort_2(L, pivot + 1, j)
def quicksort_2(L):
"""Sort list L."""
_quicksort_2(L, 0, len(L))




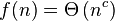
 , then
, then 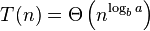

 then
then 
 then
then 